Парадокс девочки и мальчика
В теории вероятностей этот парадокс также называют «Дети мистера Смита» или «Проблемы миссис Смит». Впервые он был сформулирован американским математиком Мартином Гарднером в одном из номеров журнала «Scientific American». Учёные спорят над парадоксом уже несколько десятилетий и существует несколько способов его разрешения. Поразмыслив над проблемой, вы можете предложить и свой собственный вариант.
В семье есть двое детей и точно известно, что один из них — мальчик. Какова вероятность того, что второй ребёнок тоже имеет мужской пол? На первый взгляд, ответ вполне очевиден — 50 на 50, либо он действительно мальчик, либо девочка, шансы должны быть равными. Проблема в том, что для двухдетных семей существует четыре возможных комбинации полов детей — две девочки, два мальчика, старший мальчик и младшая девочка и наоборот — девочка старшего возраста и мальчик младшего. Первую можно исключить, так как один из детей совершенно точно мальчик, но в таком случае остаются три возможных варианта, а не два и вероятность того, что второе чадо тоже мальчик — один шанс из трёх.
Проклятая бутылка Стивенсона
Еще одна сказка, написанная Робертом Льюисом Стивенсоном, под названием «Сатанинская бутылка», знакомит читателя со спокойным гавайцем Кэаве, который приобретает бутылку с чертом, исполняющим абсолютно любые желания. Взамен этого владелец бутылки после смерти должен попасть в ад, если только ему не удастся продать эту бутылку дешевле, чем он приобрел ее сам. Парадокс здесь заключается в том, что, запросив за нее, например, 50 рублей, продать ее можно в принципе кому угодно. Но главным условием черта было совершение честного договора, то есть новый покупатель должен будет знать о таких последствиях. По словам автора, такая книга ранее стоила огромных денег, а владел ей даже сам Наполеон. То есть, даже если попытаться приобрести ее за максимальную сумму, то средств может просто напросто не хватить, да и найти покупателя будет крайне сложно, ведь чем больше сумма, тем меньше ценность такой бутылки.

Автор данной сказки решил эту задачу довольно простым образом. Выбор решения состоял из трех опций: сделка с использованием курса валюты других стран, самопожертвование (допустим, близкий родственник или любимый человек решается приобрести данную бутылку, чтобы снять проклятие), и последнее — алчный покупатель с безразличием к жизни после смерти. Несмотря на это, данная задача и по сей день считается одним из самых интересных логических парадоксов.
Дело Рональда Опуса
Не совсем логический парадокс, но эта история заслуживает того, чтобы быть в этом списке. Ее придумал Дон Харпер Миллс, бывший президент Американской Академии судебной медицины, чтобы продемонстрировать, как .
Однажды в морг привезли тело Рональда Опуса – мужчина умер от выстрела в голову из дробовика. Странное обстоятельство: Опус был застрелен при падении с вершины 10-этажного здания. Фактически Опус намеревался покончить жизнь самоубийством, выпрыгнув из окна и оставив записку, в которой объявлял о своих намерениях.
Ни стрелок, ни Опус не знали, что внизу здания была устроена страховочная сетка для безопасности промышленных альпинистов. Так что, если бы Опуса не застрелили, он, скорее всего, выжил бы после падения.
Если бы Опус намеревался совершить самоубийство и получил смертельные травмы, его смерть была бы признана самоубийством. Однако тот факт, что попытка самоубийства Опуса провалилась бы, если бы не выстрел из дробовика, заставил следователей классифицировать дело, как убийство.
По мере расследования ситуация становилась еще более странной.
Выстрел раздался из квартиры на 9-м этаже здания – там ссорилась пожилая пара. У старика была привычка махать ружьем перед женой, когда он сильно злился. В этот раз он был так разгневан, что его руки дрожали и он не мог держать ружье ровно. Когда он нажал на курок, пуля не задела его жену, она прошла через окно и попала в Опуса, который падал мимо окна.
Если старик намеревался убить свою жену, но вместо этого убил Рональда Опуса, то он виновен в смерти Опуса. Это убийство. Но после сбора показаний старика и старухи стало очевидным, что ни мужчина, ни его жена не знали, что ружье было заряжено. Поскольку старик не собирался убивать старуху, выстрел из ружья был случайным, как и смерть Рональда Опуса.
Дело закрыто? Нет! Свидетельница рассказала, что несколько недель назад она видела, как сын старика заряжал дробовик. Сын был в ярости из-за того, что мать лишила его финансовой поддержки. Зная о причудливой привычке своего отца угрожать матери дробовиком, он зарядил оружие, ожидая, что во время следующей семейной ссоры старик убьет свою жену. Теперь сын стал виновным в смерти Рональда Опуса.
Если вам кажется, что это конец истории, – не спешите. Рональд Опус решил покончить жизнь самоубийством, потому что был подавлен своей неудачной попыткой заставить отца убить мать. Да, сын, который зарядил дробовик, был не кто иной, как сам Рональд Опус!
Самые невероятные парадоксы
7. Пилоты могут “выйти” из боевого режима, если они психологически непригодны, но каждый, кто хочет “выйти” из боевого дежурства, доказывает, что он нормален.
“Уловка -22” – это сатирический роман о Второй мировой войне Джозефа Хеллера (Joseph Heller), в котором описывается ситуация, когда кто-то нуждается в чём-то, что можно получить только тогда, когда он в этом не нуждается.
Это так называемый парадокс саморефенеции. Главный герой романа Йоссариан столкнулся с этим парадоксом при оценке пилотной деятельности, но в итоге, куда бы он направлялся, он везде видел парадоксальные и репрессивные правила.
8. В каждой цифре есть что-то интересное.
1 – это первое ненулевое натуральное число, 2 – наименьшее простое число, 3 – первое нечётное простое число, 4 – наименьшее составное число и т.д. Когда вы наконец доберетесь до числа, которое покажется вам неинтересным, то это число окажется интересным из-за того, что оно показалось вам неинтересным.
Парадокс интересного числа основан на неточном определении слова “интересный”, что делает его несколько более глупым вариантом гетерологического парадокса и парадокса Рассела, которые полагаются на противоречивые самореференции.
Исследователь квантовых вычислений Натаниэль Джонстон (Nathaniel Johnston) нашёл умное решение парадокса. Вместо того, чтобы полагаться на интуитивное понятие слова “интересно”, как в исходном парадоксе, он определил интересное целое число как таковое, появляющееся в онлайн энциклопедии целочисленных последовательностей.
А это наборы из десятков тысяч математических последовательностей, таких как простые числа, числа Фибоначчи, пифагорейские тройки и т.д.
Исходя из этого определения, первое неинтересное число, наименьшее целое число, которое не отображалось ни в одной из последовательностей, – 11 630. Так как в энциклопедию на постоянной основе добавляются новые последовательности, некоторые из них включают в себя бывшие ранее неинтересными цифры.
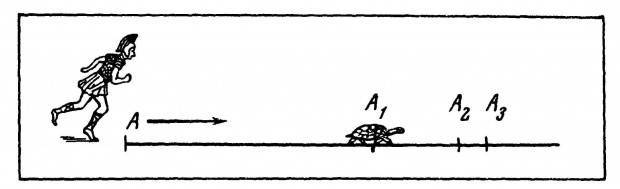
Апория «Ахиллес и черепаха»
Парадокс Ахиллеса и черепахи — одна из апорий (логически верных, но противоречивых высказываний), сформулированных древнегреческим философом Зеноном Элейским в V-м веке до нашей эры. Суть её в следующем: легендарный герой Ахиллес решил посоревноваться в беге с черепахой. Как известно, черепахи не отличаются прыткостью, поэтому Ахиллес дал сопернику фору в 500 м. Когда черепаха преодолевает эту дистанцию, герой пускается в погоню со скоростью в 10 раз большей, то есть пока черепаха ползёт 50 м, Ахиллес успевает пробежать данные ей 500 м форы. Затем бегун преодолевает следующие 50 м, но черепаха в это время отползает ещё на 5 м, кажется, что Ахиллес вот-вот её догонит, однако соперница всё ещё впереди и пока он бежит 5 м, ей удаётся продвинуться ещё на полметра и так далее. Дистанция между ними бесконечно сокращается, но по идее, герою так и не удаётся догнать медлительную черепаху, она ненамного, но всегда опережает его.
Конечно, с точки зрения физики парадокс не имеет смысла — если Ахиллес движется намного быстрее, он в любом случае вырвется вперёд, однако Зенон, в первую очередь, хотел продемонстрировать своими рассуждениями, что идеализированные математические понятия «точка пространства» и «момент времени» не слишком подходят для корректного применения к реальному движению. Апория выявляет расхождение между математически обоснованной идеей, что ненулевые интервалы пространства и времени можно делить бесконечно (поэтому черепаха должна всегда оставаться впереди) и реальностью, в которой герой, конечно, выигрывает гонку.
Удивительные парадоксы
5. Существует бесконечно длинный “рог”, которые имеет конечный объём, но бесконечную площадь поверхности.
Двигаясь навстречу проблеме, появившейся в 17 веке, мы получаем один из многих парадоксов, связанных с геометрией и бесконечностью.
“Рог Гавриила” формируется путём взятия кривой y = 1/х и поворота вокруг горизонтальной оси, как показано на рисунке.
Используя методы исчисления, которые позволяют вычислить площади и объёмы построенных таким образом фигур, можно видеть, что бесконечно длинный рог фактически имеет конечный объём, равный числу пи, но бесконечную площадь поверхности.
Иными словами, в рог поместится определённое количество краски, но для того, чтобы покрыть краской всю его поверхность, потребуется её бесконечное количество.
6. Гетерологическое слово – это слово, которое не описывает себя. А описывает ли себя слово “гетерологический”?
Это один из многих парадоксов, который долго томил умы современных математиков и логиков.
Примером гетерологического слова может быть слово “глагол”, которое не является глаголом по сути (в отличие от “существительного”, которое является существительным). Другим примером может быть слово “длинный”, которое не является длинным словом (в отличие от слова “короткий”, которое является коротким словом).
Так “гетерологический” является гетеролигическим словом или нет? Если бы это было бы слово, которое не описывает себя, тогда оно бы описывало себя. А если бы оно было словом, которое описывает себя, оно бы не описывало себя.
Это связано с парадоксом Рассела, который спрашивает, содержит ли определённое множество себя в качестве элемента.
Создавая подобные самоуничтожающиеся множества, Бертран Рассел (Bertrand Russell) и другие учёные продемонстрировали важность установления тщательных правил при создании множеств, которые заложили основу математики 20 века
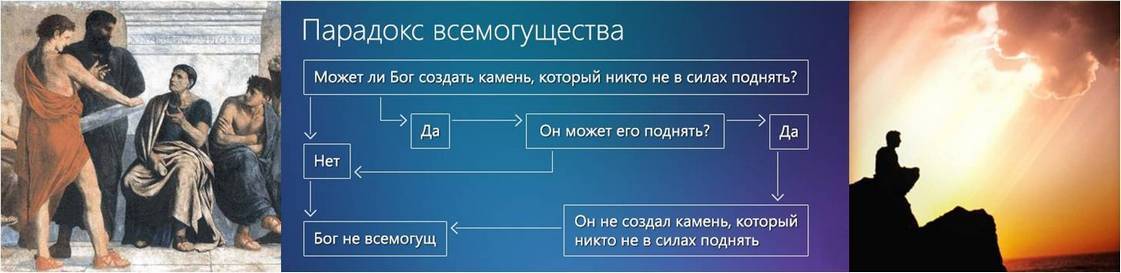
Парадокс всемогущества
Суть этого парадокса связана со следующим вопросом: способен ли Всемогущий создать камень, который он был бы не в силах поднять? То есть, если Всемогущий может создать такой камень, но не может его поднять, то его могущество становится спорным. А если же он не может создать такой камень, то опять же его всемогущество ставится под вопрос. Отвечая на этот вопрос, некоторые философы утверждали, что Бог не может создать ситуацию, при которой он подверг бы сомнению свое могущество. А другие утверждали, что существование Всемогущего не может быть воспринято человеческим разумом и находится вне человеческой логики.
Парадокс лжеца
1Gai.Ru / hereticwear.com
Это хорошо известный парадокс, который сформулировал великий философ-стоик Хрисипп. Говорят, поэт, грамматист и критик Филит Косский умер от истощения, пытаясь решить эту проблему.
Критянин приплыл в Грецию и сказал грекам на берегу: «Все критяне – лжецы». Что он сказал: правду или ложь? Неделей позже критянин снова приплыл в Грецию и произнес: «Все критяне – лжецы, а все, что я говорю, – правда». Греки на берегу так и не поняли, сказал ли гость правду в первый раз, поэтому они были по-настоящему озадачены.
Если кто-то говорит: «Я всегда лгу», говорит ли он правду? Или он обманывает, как и сказал?
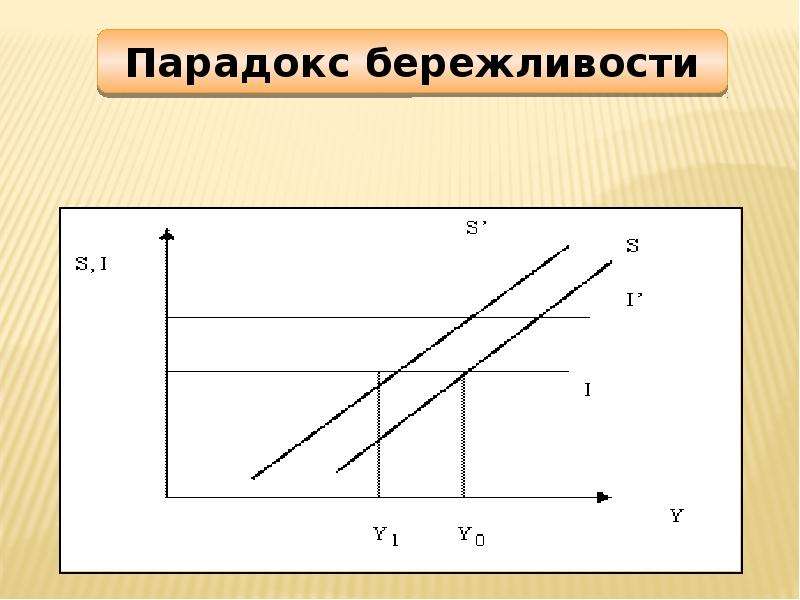
Парадокс бережливости
Многие знают изречение Брежнева о том, что экономика должна быть экономной. Но не всегда экономия приносит пользу. Если все люди вместе станут экономить в период кризиса, то это приведет к снижению спроса товаров, после чего последует разорение фирм и, соответственно, снижение зарплат в совокупности с ростом безработицы. Таким образом, формируется некий якорь, который как бы «тащит» экономику вниз. Однако существует и иное мнение. В классической модели экономики подразумевается, что чем больше доходов идет на сбережение, тем значительней становятся темпы роста экономики в целом.
Интересные парадоксы
3. Если вы восстановили корабль, заменив все его деревянные части, это остался тот же корабль?
Ещё один классический парадокс из Древней Греции, “Корабль Тесея” – это парадокс о противоречиях идентичности. Его хорошо описал Плутарх.
Корабль, на котором Тесей и молодёжь Афин возвращались с Крита, имел 30 весёл, которые были сохранены вплоть до времён Димитрия Фалерея. А всё благодаря тому, что когда старые деревянные доски начали разлагаться, их заменили на новые, более крепкие.
Они держались так долго, что этот корабль стал постоянной темой обсуждения среди философов, которые говорили о логике разных вещей, которые изменяются. Одна группа философов говорила, что корабль остался тем же, в то время, как другие философы настаивали, что после замены брёвен, корабль стал другим.
4. Может ли Всемогущий создать скалу, слишком тяжёлую для того, чтобы он сам мог её поднять?
Как может существовать зло, если Бог всемогущ? Как можем мы называть себя свободными, если Бог всеведущ?
Это лишь несколько из многих существующих парадоксов, касающихся применения вопросов логики к божественной теме.
Некоторые люди могут ссылаться на эти парадоксы, объясняя тем самым, почему они не верят в высшее существо. Однако, другие говорят, что они несущественны и по разным причинам не работают.
Почему важно развивать логическое мышление?
Развитая логика — это возможность правильно анализировать различные ситуации и принимать верные решения. Применение логики в жизни позволяет быстро распознавать обман, эффективно работать с большими объемами информации, решать массу сложных задач. Всё это говорит о том, что работа над логическим мышлением необходима человеку. У Викиум есть специальный курс для этого — «Мышление Шерлока». Кроме того, на сайте можно найти много интересных и полезных тренажеров, также направленных на развитие логики. Умение мыслить логически не дается просто так, этому нужно учиться. Поэтому советуем не терять время!
Парадокс воронов
Проблема также известна, как парадокс Гемпеля — второе название она получила в честь немецкого математика Карла Густава Гемпеля, автора её классического варианта. Проблема формулируется довольно просто: каждый ворон имеет чёрный цвет. Из этого следует, что всё, что не чёрного цвета, не может быть вороном. Этот закон называется логическая контрапозиция, то есть если некая посылка «А» имеет следствие «Б», то отрицание «Б» равнозначно отрицанию «А». Если человек видит чёрного ворона, это укрепляет его уверенность, что все вороны имеют чёрный окрас, что вполне логично, однако в соответствии с контрапозицией и принципом индукции, закономерно утверждать, что наблюдение предметов не чёрного цвета (скажем, красных яблок) также доказывает, что все вороны окрашены в чёрный цвет. Иными словами — то, что человек живёт в Санкт-Петербурге доказывает, что он живёт не в Москве.
С точки зрения логики парадокс выглядит безукоризненно, однако он противоречит реальной жизни — красные яблоки никоим образом не могут подтверждать тот факт, что все вороны чёрного цвета.
- Любопытные факты про Францию, Гитлера и китайских мужчин
- Француз весом 50 кг, способный съесть всё, что угодно
- Мыслеграфия — надувательство XIX века, которое приносило деньги
- Отломите лезвие канцелярского ножа при помощи заглушки на самом ноже
- Любопытные факты о вулканах на нашей планете и за её пределами
Парадокс крокодила
howitworkshour.blogspot.com
Этот древний логический парадокс приписывается сицилийцу Кораксу.
Крокодил выхватывает из рук египтянки мальчика. Мать умоляет хищника вернуть сына, на что крокодил отвечает: он вернет мальчика, только если мать правильно угадает, сделает он это или нет. Если женщина права – мальчика возвращают. Если нет – крокодил забирает сына.
Допустим, женщина ответит, что крокодил не отдаст ее сына. Тогда получаем парадокс: если она права и крокодил никогда не намеревался вернуть ее ребенка, то крокодил должен его вернуть.
Однако тем самым он нарушает свое слово и противоречит ответу матери. С другой стороны, если мать ошибается и крокодил действительно хотел вернуть мальчика, животное должно оставить ребенка, даже если оно не собиралось этого делать, тем самым вновь нарушая свое слово.
Парадокс временной петли
Парадоксы, описывающие путешествия во времени, давно служат источником вдохновения для писателей-фантастов и создателей научно-фантастических фильмов и сериалов. Существует несколько вариантов парадоксов временной петли, один из самых простых и наглядных примеров подобной проблемы привёл в своей книге «The New Time Travelers» («Новые путешественники во времени») Дэвид Туми, профессор из Университета Массачусетса.
Представьте себе, что путешественник во времени купил в книжном магазине экземпляр шекспировского «Гамлета». Затем он отправился в Англию времён Королевы-девы Елизаветы I и отыскав Уильяма Шекспира, вручил ему книгу. Тот переписал её и издал, как собственное сочинение. Проходят сотни лет, «Гамлета» переводят на десятки языков, бесконечно переиздают, и одна из копий оказывается в том самом книжном магазине, где путешественник во времени покупает её и отдаёт Шекспиру, а тот снимает копию и так далее… Кого в таком случае нужно считать автором бессмертной трагедии?
Самые интересные парадоксы
9. В баре всегда есть хотя бы один клиент, для которого верно, что если пьёт он, значит пьют все.
Условные утверждения в формальной логике иногда имеют противоречивые интерпретации, а парадокс пьянства – отличный тому пример. На первый взгляд, парадокс предполагает, что один человек заставляет пить остальную часть бара.
Фактически всё это говорит о том, что было бы невозможно, чтобы все в баре пили, если бы каждый отдельно взятый клиент не пил. Поэтому там есть по крайней мере один клиент (то есть последний, который не пьёт), который выпив, мог бы сделать так, чтобы можно было сказать, что пьют все.
10. Из мяча, который можно разрезать на конечное число частей, реально сделать два других мяча одинакового размера.
Парадокс Банаха-Тарского опирается на множество странных и противоречивых свойств бесконечных множеств и геометрических вращений.
Части, на которые можно разрезать мяч, будут выглядеть очень странно, поэтому парадокс работает только в абстрактной математической сфере. Было бы отлично, если можно было взять, к примеру, яблоко, разрезать его на части и собрать два одинаковых, но меньшего размера, чтобы поделиться с другом.
Но физические “шары” из материального мира не могут быть разобраны как математическая сфера.
Апория «Летящая стрела»
Знаменитый парадокс Зенона Элейского затрагивает глубочайшие противоречия в представлениях учёных о природе движения и времени. Апория сформулирована так: стрела, выпущенная из лука, остаётся неподвижной, так как в любой момент времени она покоится, не совершая перемещения. Если в каждый момент времени стрела покоится, значит она всегда находится в состоянии покоя и не движется вообще, так как нет момента времени, в который стрела перемещается в пространстве.

Выдающиеся умы человечества веками пытаются разрешить парадокс летящей стрелы, однако с логической точки зрения он составлен абсолютно верно. Для его опровержения требуется объяснить, каким образом конечный временной отрезок может состоять из бесконечного числа моментов времени — доказать это не удалось даже Аристотелю, убедительно критиковавшему апорию Зенона. Аристотель справедливо указывал, что отрезок времени нельзя считать суммой неких неделимых изолированных моментов, однако многие учёные считают, что его подход не отличается глубиной и не опровергает наличие парадокса. Стоит отметить, что постановкой проблемы летящей стрелы Зенон стремился не опровергнуть возможность движения, как таковую, а выявить противоречия в идеалистических математических концепциях.
Парадокс Ахиллеса и черепахи
Этот парадокс – одно из парадоксальных рассуждений древнегреческого философа Зенона.
Ахиллес бросает вызов черепахе в состязании по бегу. Чтобы все было по-честному, он соглашается дать черепахе фору, скажем, в 1000 шагов. Когда начинается гонка, Ахилл, что неудивительно, начинает бежать со скоростью, намного превышающей скорость черепахи. Но за то время, за которое Ахиллес пробежит 1000 шагов, черепаха проползет еще 100 шагов в ту же сторону.
 makeagif.com
makeagif.com
Когда Ахиллес пробежит 100 шагов – черепаха проползет еще 10 и так далее. Таким образом, процесс будет продолжаться до бесконечности, и Ахиллес никогда не сможет догнать животное.
Следовательно, быстроногий герой никогда не догонит неторопливую черепаху, если в начале движения она будет находиться впереди него.
Обложка: Shutterstock
Источник статьи: What are some good logical paradoxes?
Парадокс воронов
Карл Густав Гемпель — это философ, который интересно объясняет данный парадокс. Предположим, что каждый ворон черного цвета. Следуя простой логике, все не являющиеся чёрными предметы не будут считаться воронами. Чем больше человек увидит черных воронов, тем сильнее закрепится в его сознании, что все вороны одинакового цвета. Увидев же коричневых коров, белых медведей и синие ели человек только усилит свое мнение о том, что все не являющиеся чёрными предметы — это не вороны. Но подобный вывод в корне противоречит интуитивному восприятию реальности. Если же человек натолкнется на белого медведя, в большей вероятности, это увеличит уверенность в том, что все не являющиеся чёрными предметы не будут считаться воронами, но при этом вряд ли это заставит его думать, что все вороны обязательно должны быть черного цвета.
Софизм «Крокодил»
На берегу реки стоят мать с ребёнком, вдруг к ним подплывает крокодил и затаскивает ребёнка в воду. Безутешная мать просит вернуть её чадо, на что крокодил отвечает, что согласен отдать его целым и невредимым, если женщина правильно ответит на его вопрос: «Вернёт ли он её ребёнка?». Понятно, что у женщины два варианта ответа — да или нет. Если она утверждает, что крокодил отдаст ей ребёнка, то всё зависит от животного — посчитав ответ правдой, похититель отпустит ребёнка, если же он скажет, что мать ошиблась, то ребёнка ей не видать, согласно всем правилам договора.
Отрицательный ответ женщины всё значительно усложняет — если он оказывается верным, похититель должен выполнить условия сделки и отпустить дитя, но таким образом ответ матери не будет соответствовать действительности. Чтобы обеспечить лживость такого ответа, крокодилу нужно вернуть ребёнка матери, но это противоречит договору, ведь её ошибка должна оставить чадо у крокодила.
Стоит отметить, что сделка, предложенная крокодилом, содержит логическое противоречие, поэтому его обещание невыполнимо. Автором этого классического софизма считается оратор, мыслитель и политический деятель Коракс Сиракузский, живший в V-м веке до нашей эры.
Корабль Тесея
Тесей – герой греческой мифологии, который совершил много благородных поступков. Согласно мифу, корабль, на котором Тесей вернулся с Крита в Афины, афиняне сохранили как памятник его героизму.
Конечно, корабль был сделан из дерева, железа и веревки – материалов, которые со временем разрушаются водой. Поскольку деревянные доски и веревки гнили, а железные крепления ржавели, греки меняли их по частям. В конце концов все части корабля были заменены. А теперь вопрос: это все еще корабль Тесея?
Если вы скажете «да», то подумайте вот над чем: что, если бы из оригинальных деталей, которые были демонтированы, собрали новый корабль? Тогда получится два корабля: один будет сделан из совершенно новых частей, а другой – из оригинальных частей корабля Тесея. Будете ли вы все еще утверждать, что корабль из новых деталей – это корабль Тесея?
Если вы скажете: «Нет, это не тот корабль», подумайте: в какой момент он перестает быть кораблем Тесея? Когда заменят первую часть? Или последнюю деталь? Быть может, когда заменят больше половины? Ведь должен же наступить момент, когда судно перестанет быть кораблем Тесея.
Образование новых штатов
Число представителей от старых штатов может изменяться с появлением еще одного штата. Этот парадокс был обнаружен еще в начале двадцатого века во времена, когда Оклахома отделилась и стала самостоятельной. Прежде Палата представителей состояла из 386 мест. В соответствии с населением Оклахомы было решено выделить для данного штата 5 мест. Исходя из этого, общее число мест Палаты стало 391. Однако при этом предполагалось, что число мест других штатов останется прежним. Но в результате пропорционально-территориального распределения мест штат Мэн получил дополнительное представительское место, а Нью-Йорк, в свою очередь одного места лишился.
Карточный парадокс
1Gai.Ru / wikipedia.org
Представьте, что вы держите в руке карточку, на одной стороне которой написано: «Утверждение на другой стороне этой карточки верно».
Назовем его Утверждением А. Переверните карточку, и на противоположной стороне будет написано: «Утверждение на другой стороне этой карточки ложно» (Утверждение Б). Однако попытка приписать «истину» утверждению A или Б приводит к парадоксу: если A истинно, то Б также должно быть истинным. Но для того чтобы Б было истинным, A должно быть ложным. И наоборот – если A ложно, то Б тоже должно быть ложным, что в итоге должно сделать A истинным.
Карточный парадокс, изобретенный британским логиком Филипом Журденом в начале 1900-х годов, – это простое объяснение уже знакомого нам парадокса лжеца, при котором приписывание значений истинности утверждениям, которые претендуют на то, чтобы быть истинными или ложными, приводит к противоречию.
Парадокс лотереи
Сара Лоуренс / vox.com
Он был сформулирован профессором Рочестерского университета Генри Кайбергом.
Предположим, вы покупаете лотерейный билет. В вечерних новостях вы слышите, что было продано 1000 билетов и что победитель будет определен из общего числа проданных экземпляров.
И все же вы знаете, что вероятность вашего выигрыша слишком мала. У вас есть все основания полагать, что ваш билет не выиграет. Равно как и билет вашего дяди, вашей бабушки, сестры или друга. И так вплоть до 1000-го. Это равносильно признанию того, что ни один билет не выиграет.
Получается противоречие: один билет должен быть выигрышным и в то же время никакой билет не может выиграть.
Парадокс мешка картофеля
Допустим, у некоего фермера имеется мешок картофеля весом ровно 100 кг. Изучив его содержимое, фермер обнаруживает, что мешок хранился в сырости — 99% его массы составляет вода и 1% остальные вещества, содержащиеся в картофеле. Он решает немного высушить картофель, чтобы содержание воды в нём снизилось до 98% и переносит мешок в сухое место. На следующий день оказывается, что, один литр (1 кг) воды действительно испарился, но вес мешка уменьшился со 100 до 50 кг, как такое может быть? Давайте посчитаем — 99% от 100 кг это 99 кг, значит соотношение массы сухого остатка и массы воды изначально было равно 1/99. После сушки вода насчитывает 98% от общей массы мешка, значит соотношение массы сухого остатка к массе воды теперь составляет 1/49. Так как масса остатка не изменилась, оставшаяся вода весит 49 кг.
Конечно, внимательный читатель сразу обнаружит грубейшую математическую ошибку в расчётах — мнимый шуточный «парадокс мешка картофеля» можно считать отличным примером того, как с помощью на первый взгляд «логичных» и «научно подкреплённых» рассуждений можно буквально на пустом месте выстроить теорию, противоречащую здравому смыслу.